Tekil Değer Ayrışımı - 1

Bu yazı, tekil değer ayrışımı üstüne yazacağım bir yazı dizisinin ilk yazısı. Bu konuyu seçme sebebim hem şu anki çalışmalarımın özünü oluşturması, hem de konunun önemi.

Tekil değer ayrışımı (TDA) [Singular Value Decomposition - SVD], bir matrisin çarpanlarına ayrılma türlerinden biridir ve Google'ın PageRank algoritmasından insan yüzlerini modellemeye, otomatik deneme notlamasından gen analizine, bilgi getirimi ve çıkarımından boyut azaltma (ör: temel bileşenler analizi) ve veri sıkıştırmaya kadar uzanan geniş bir yelpazede kullanılan temel adımdır.

Bu yazıda TDA'nın matematiksel temellerini sunup uygulamaya yönelik kısımlarını ve yorumlarını daha sonraki yazılara bırakacağım.

Matematiksel ifadeler: Skalerler küçük harflerle yazılır, ör: $a$. Vektörler kalın küçük harflerle yazılır, ör: $\mathbf{a}$. $\mathbf{a}$ vektörünün $i$ indisindeki elemanı $a_i$ olarak gösterilir. Matrisler kalın büyük harflerle yazılır, ör: $\mathbf{A}$. $\mathbf{A}$'nın $j$. sütunu $\mathbf{a}_j$ vektörü olarak, $(i,j)$ hücresindeki elemanı ise $a_{ij}$ olarak ifade edilir. ${}^H$ işareti Hermit (karmaşık) transpozu göstermek üzere kullanılır. $\mathbf{a} \in \mathbb{C}^I$ vektörünün $L_2$ normu (veya Öklit normu) $\| \cdot \|_2$ sembolleri ile gösterilir ve şöyle tanımlanır:

$$
\| \mathbf{a} \|_2 := \sqrt{ |a_1|^2 + \dots + |a_I|^2 } = \sqrt{(\mathbf{a}^{H} \mathbf{a})}
$$

$\mathbf{A} \in \mathbb{C}^{I\times J}$ matrisinin spektral normu, benzer şekilde $\| \cdot \|_2$ sembolleri ile gösterilir ve $\mathbf{A}^H\mathbf{A}$ matrisinin en büyük özdeğerinin kareköküne eşittir:

$$
\begin{align}\| \mathbf{A} \|_2 & := \mathbf{A}^H\mathbf{A} \text{ matrisinin en büyük özdeğerinin karekökü} \\ & = \max\limits_{\|\mathbf{x}\|_2 \neq 0}{\frac{\|\mathbf{Ax}\|_2}{\|\mathbf{x}\|_2}} \end{align}
$$

Dikey (orthogonal) $\mathbf{A} \in \mathbb{C}^{I\times J}$ matrisinin farklı sütunlarının iç çarpımları sıfırdır. Sütun normları 1 olan dikey matrise birim dikey (orthonormal) matris denir. Aynı zamanda matris kare ise, üniter (unitary) matris olarak adlandırılır ve $\mathbf{A}^H\mathbf{A} = \mathbf{A}\mathbf{A}^H = \mathbf{I}$ denkliğini sağlar.

Teorem (Tekil Değer Ayrışımı)

Her $\mathbf{A} \in \mathbb{C}^{I\times J}$ matrisini

$$\mathbf{A} = \mathbf{U}\mathbf{\Sigma} \mathbf{V}^{H} $$

biçiminde alttaki maddeleri sağlayacak şekilde çarpanlarına ayırabiliriz.

• $\mathbf{U} = \left[ \begin{array}{cccc} \mathbf{u}_{1} & \mathbf{u}_{2} & \dots & \mathbf{u}_{I} \end{array} \right] \in \mathbb{C}^{I\times I}$ üniter bir matristir.
• $\mathbf{V} = \left[ \begin{array}{cccc} \mathbf{v}_{1} & \mathbf{v}_{2} & \dots & \mathbf{v}_{J} \end{array} \right] \in \mathbb{C}^{J\times J}$ üniter bir matristir.
• $\mathbf{\Sigma} \in \mathbb{C}^{I\times J}$ sözdeköşegen (pseudodiagonal) bir matristir $\newcommand{\diag}{\mathop{\mathrm{köşegen}}}\mathbf{\Sigma} = \diag \left(\ \sigma_1, \sigma_2, \dots, \sigma_{\min(I,J)} \right) $ ve sıralıdır $(\sigma_1 \geq \sigma_2 \geq \ldots \geq \sigma_{\min(I, J)} \geq 0$.

Kanıt

$\sigma = \|\mathbf{A}\|_2$ olacak şekilde $\mathbf{A}\mathbf{x} = \sigma \mathbf{y}$ denklemini sağlayan $\mathbf{x} \in \mathbb{C}^{J}$ ve $\mathbf{y}\in \mathbb{C}^{I}$ birim vektörlerini ($\|\mathbf{x}\|_2 = \|\mathbf{y}\|_2 =1$) alalım. Bu vektörler $\mathbf{V}$ ve $\mathbf{U}$ dikey matrislerinin birinci sütun vektörleri olsunlar;

$$\mathbf{U} = \left[ \begin{array}{cc} \mathbf{y} & \mathbf{\hat{U}} \end{array} \right] \in \mathbb{C}^{I \times I}$$

$$\mathbf{V} = \left[ \begin{array}{cc} \mathbf{x} & \mathbf{\hat{V}} \end{array} \right] \in \mathbb{C}^{J \times J}$$

Şimdi $\mathbf{U}^H \mathbf{A} \mathbf{V}$ çarpımına bakalım:

$$
\begin{align}
\mathbf{\hat{A}} & = \mathbf{U}^H\mathbf{A}\mathbf{V} \\
& = \left[ \begin{array}{cc}\mathbf{y} & \mathbf{\hat{U}} \end{array}\right]^H \mathbf{A} \left[ \begin{array}{cc} \mathbf{x} & \mathbf{\hat{V}} \end{array} \right] \\
& = \left[ \begin{array}{c} \mathbf{y}^H \\ \mathbf{\hat{U}}^H \end{array} \right] \mathbf{A} \left[ \begin{array}{cc} \mathbf{x} & \mathbf{\hat{V}} \end{array} \right] \\
& = \left[\begin{array}{cc}\mathbf{y}^H \mathbf{A} \mathbf{x}  & \mathbf{y}^H \mathbf{A} \mathbf{\hat{V}} \\ \mathbf{\hat{U}}^H \mathbf{A} \mathbf{x} & \mathbf{\hat{U}}^H \mathbf{A} \mathbf{\hat{V}} \end{array} \right] \end{align}$$

Elde ettiğimiz $\mathbf{\hat{A}}$ matrisinin blok blok elemanlarına bakalım. $\mathbf{A} \mathbf{x} = \sigma \mathbf{y} \Rightarrow \mathbf{y}^H \mathbf{A} \mathbf{x} = \sigma$, yani sol üst blok $\sigma$. Sadelik olsun diye sağ üst bloğa $\mathbf{w}^H$ diyelim. Yani, $\mathbf{w}^H = \mathbf{y}^H \mathbf{A} \mathbf{\hat{V}}$. Yine işleri sadeleştirmek için sağ alt bloğa $\mathbf{B}$ diyelim, yani $\mathbf{B} = \mathbf{\hat{U}}^H \mathbf{A} \mathbf{\hat{V}}$. Şimdi sol alt bloğa bakalım.

$$\mathbf{\hat{U}}^H \mathbf{A} \mathbf{x} = \lambda \mathbf{\hat{U}}^H \mathbf{y} = \mathbf{0} $$

çünkü $\mathbf{U}$ matrisi dikey, başka bir deyişle $\mathbf{y}$ diğer tüm sütun vektörlere dik.

Çarpım bir hayli sadeleşti:

$$\mathbf{\hat{A}} = \begin{array}{cc} & \\ \left[\begin{array}\ \sigma & \mathbf{w}^H \\ \mathbf{0} & \mathbf{B} \end{array} \right] & \begin{array}{c} 1\\ I-1 \end{array} \\ \begin{array}{c}& &1 & J-1 & \end{array} & \end{array}$$

Tam bu noktada bir es verip ne durumda olduğumuza bakalım. Tanımımızı (dış çarpanların üniter matris ve iç çarpanın köşegen matris oluşu) ne kadar gerçekledik? $\mathbf{U}$ ve $\mathbf{V}$ matrisleri için koşulları sağladığımızı varsaydık ve sol alt blok sıfırlardan oluştu. Peki sağ üst blok, yani $\mathbf{w}^H$? O da sıfır çıkarsa, benzer şekilde devam ederiz ve tümevarımla köşegen dışındaki elemanların sıfırlardan oluşması gerektiğini göstermiş oluruz. Hatta $\|\mathbf{A}\|_2 \geq \|\mathbf{B}\|_2$ olacağından sıralı olma durumunu da sağlamış oluruz. Yani işimiz $\mathbf{w}^H$ satır vektörünün sıfırlardan oluşmasına kaldı.

Bunu kanıtlamak için normlardan yararlanacağız. Öncelikle dikey dönüşümlerde spektral normun değişmeyeceğini, çünkü en büyük özdeğerin bu dönüşümlerden etkilenmeyeceğini göz önünde tutarak $\|\mathbf{\hat{A}}\|_2 = \|\mathbf{A}\|_2 = \sigma$ olacağını bilelim. Şimdi, Cauchy–Schwarz eşitsizliğinin matrise genellenmişini ($\|\mathbf{A}\|_2 \|\mathbf{x}\|_2 \geq \|\mathbf{Ax}\|_2$) kullanırsak

$$\left\| \mathbf{\hat{A}} \right\|_2^2 \left\| \left(\begin{array}{c}\sigma\\ \mathbf{w}\end{array} \right) \right\|_2^2 = \sigma^2 \left\| \left(\begin{array}{c}\sigma\\ \mathbf{w}\end{array} \right) \right\|_2^2 = \sigma^2 (\sigma^2 + \mathbf{w}^H \mathbf{w}) \geq  \left\| \mathbf{\hat{A}} \left(\begin{array}{c}\sigma\\ \mathbf{w}\end{array} \right) \right\|_2^2 $$

eşitsizliğini elde ederiz. Öte yandan

$$\left\| \mathbf{\hat{A}} \left(\begin{array}{c}\sigma\\ \mathbf{w}\end{array} \right) \right\|_2^2 =  \left\|\left[\begin{array}\ \sigma & \mathbf{w}^H \\ \mathbf{0} & \mathbf{B} \end{array} \right] \left(\begin{array}{c}\sigma\\ \mathbf{w}\end{array} \right) \right\|_2^2 \geq (\sigma^2 + \mathbf{w}^H \mathbf{w})^2 $$

eşitsizliği de açıktır. Üstteki iki eşitsizliği birleştirdiğimizde,

$$\sigma^2 \geq (\sigma^2 + \mathbf{w}^H \mathbf{w}) \tag{7}$$

çıkar ve bu $\mathbf{w}^H\mathbf{w}$ değerinin 0 olmasını, yani $\mathbf{w}$ vektörünün tüm değerlerinin sıfır olmasını gerektirir. Tümevarımla, sıradaki büyük özdeğeri seçerek ilerlersek iç çarpan köşegenleştirilebilir ve verdiğimiz koşulları sağlayan bir ayrışım yapmış oluruz.

* * *

Şimdi ortamı biraz şenlendirelim; biraz açıklık kazanması amacıyla $\mathbf{A} \in \mathbb{R}^{2 \times 2}$ için bunu görselleştirelim. Dikkat ederseniz kanıtı $\mathbf{A}$ matrisinin $\mathbf{v}_j$ birim vektörlerini $\mathbf{u}_i$ birim vektörlerinin $\sigma_i$ kadar uzamış hallerine dönüştürdüğünü sezerek yaptık ($1\leq i \leq I$, $1\leq j \leq J$). 2 boyut için düşünürsek, $\mathbf{v}_j$ vektörleri bir birim çemberin iki dik vektörü olacak, dönüşümde elde edilecek $\mathbf{u}_i$ vektörleri ise bir elipsin eksenlerini oluşturacak. Daha büyük boyutlarda hiperkürenin hiperelipsoide dönüşümünü gözlemleyeceğiz. Lafı fazla uzatmadan 2 boyuttaki MATLAB örneğimize geçelim.

% Matrisi tanımlayalım
A = [ 0.3*cos(pi/6)   1.2*sin(pi/6)
      0.3* -sin(pi/6) 1.2*cos(pi/6)];

% Figür ayarlarını yapalım
fig1 = subplot(1,2,1);
hold on; axis equal; title('U')
fig2 = subplot(1,2,2);
hold on; axis equal; title('V')
linkaxes([fig1, fig2]);
axis([-1.5 1.5 -1.5 1.5])

for theta = 0:pi/150:2*pi

    % Her açı için birim çember üstünde bir x alıp, nereye düştüğüne
    % bakalım
    x = [cos(theta); sin(theta)];
    y = A*x;

    % Gittikçe beyazlaşacak şekilde çizelim
    plot(fig1, [0 y(1)], [0 y(2)], ...
        'Color', [theta/(2*pi) theta/(2*pi) theta/(2*pi)], ...
        'LineWidth', 3);
    plot(fig2, [0 x(1)], [0 x(2)], ...
        'Color', [theta/(2*pi) theta/(2*pi) theta/(2*pi)], ...
        'LineWidth', 3);
end

% Bakalım, matlab'ın bulduğu değerler nasıl gözüküyor
[U, S, V] = svd(A);

% Sol ve sağ tekil vektörleri çizelim
plot(fig1,[0 U(1,1)], [0 U(2,1)], 'Color', 'red', 'LineWidth', 3);
plot(fig1,[0 U(1,2)], [0 U(2,2)], 'Color', 'blue', 'LineWidth', 3);
plot(fig2,[0 V(1,1)], [0 V(2,1)], 'Color', 'red', 'LineWidth', 3);
plot(fig2,[0 V(1,2)], [0 V(2,2)], 'Color', 'blue', 'LineWidth', 3);

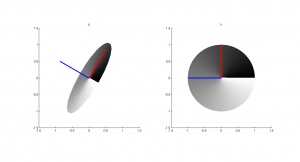
Üstteki kodda, sağa gelecek çizimdeki bir birim çemberin üstünde adım adım gezdik ve solda onun $\mathbf{A}$ matrisi tarafından nereye dönüştürüldüğünü gördük. Alışılmışın tersine sağdan sola yapmamdaki kasıt $\mathbf{U}$'nun sütunlarına literatürde sol tekil vektörler denmesi, $\mathbf{V}$'ninkilere de sağ. Yani sonradan gelecek kafa karışıklığını önlemek. Hangi vektörün nereye düştüğü anlaşılsın diye renklerini açarak çizdirdim. Sonuç şöyle:

Dönüşümlerden ziyade MATLAB'ın svd kodunu kullanarak onun bulduğu vektörleri çizdirdim. Tam olarak aradığımız vektörler çıktı ve çizimlerimize cuk oturdu! Örneğin üstteki çizime bakarsak, birim çemberin bir elipse dönüştüğünü ve aradığımız tekil değerlerin bu elipsin eksen uzunluklarının yarıları olduğu ortaya çıktı. Örnekte bu değerler 1.2 ve 0.3 olarak elde edildi. Soldaki çizimde kırmızı ve mavi doğru parçaları birim uzunlukta (bunlar $\mathbf{u}_1$ ve $\mathbf{u}_2$ vektörleri), elipsin dik eksenleri ise görüldüğü gibi 1.2 ve 0.3 katları. Zaten matrisi önce ölçekleyip sonra döndürecek şekilde özel olarak seçmiştim, sonuçta da bunları elde ettik.

Burada şunu belirtmemde yarar var; elde edilen elipsin dik eksenleri her zaman bizim birim çemberin x ve y eksenlerindeki vektörlere karşılık gelmeyebilir. Örneğin matrisi şöyle tanımlasaydık;

A = [ 0.6 0.4
        0   1];

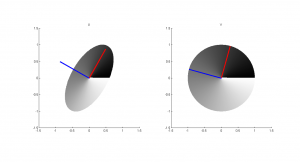
birim çemberin üstünden ve altından tutup yanlara doğru yamultmuşuz gibi bir etki yaratacaktık ve oluşacak elipsin dik eksenleri tam olarak bizim birim çemberin  x ve y eksenlerine yapışık olmayacaktı. Oluşan şekil altta:

Burada gösterilen birim çemberi daha üst boyutlarda hayal ederseniz, yani bir birim hiperkürenin yüzeyinde dolaştığınızı düşlerseniz, dönüşüm sizi bir hiperelipsoidin yüzeyine atacaktır ve bu elipsoidin dik eksenlerinin doğrultuları sağ tekil vektörler, boyları ise tekil değerler olacaktır.

Bunun tersini de düşünebilirsiniz, yani elipsten birim çembere geldiğinizi. Ya da bunun üst boyutlar için olanını. Bir elipsin, belli doğrultularında değişim fazla veya az iken (yani eksen boyları çok farklılık gösterebilirken) birim çemberde her yön bir!

İlerde bu yorumları temel bileşenler analizi ve daha birçok tekniği inşa etmek için kullanacağız. Sonraki yazıda kaldığımız yerden devam etmek üzere burada bırakalım.