Matematikte bir probleme yaklaşımda üç temel soru başat konumdadır. Üstünde kafa yorduğumuz matris ayrışımını düşünürsek, sorularımız şunlardır:

  1. Çalıştığımız uzayın tüm elemanları için bu ayrışım var mıdır? (existence)
  2. Bir eleman için ayrışım tek midir? (uniqeuness)
  3. Değerlerdeki küçük oynamalar (perturbation) ayrışım sonuçlarını ne denli etkiler? Gürültülü bir veri için sonuçlara ne denli güvenilir? Yani değerler hafif farklı olsaydı tamamen farklı sonuçlar mı alırdık, yoksa sonuçlarda küçük değişiklikler mi gözlenirdi? Özetle yöntem kararlı mıdır (stable)? Ya da başka bir deyişle problem kötü konumlanmış (ill-posed) bir problem midir?

Üstteki üç özelliği sağlayan bir problem iyi konumlanmış (well-posed) olarak da tanımlanmaktadır.

Tekil değer ayrışımı (TDA) konusuna önceki yazımızda giriş yapmıştık. Şimdi TDA için bu soruları soralım.

Herhangi bir matris için tekil değer ayrışımı yapılabileceğini göstermiştik, hatta adım adım kanıtlamıştık. Yani birinci madde cepte!

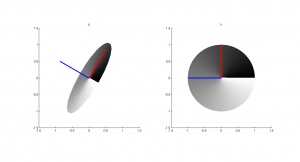
Şimdi ikinci soruya geçelim. Bir matrisin tek bir tekil değer ayrışımı mı var, yoksa birden çok çözüm olabilir mi? Önceki yazıdaki figüre bir gözatalım. Altta aynı figürü ekledim.

Hatırlarsak, sağdaki çemberin kırmızı ve mavi ile gösterilen eksenleri $\mathbf{v}_1$ ve $\mathbf{v}_2$ idi. Soldaki elipsinkiler ise $\mathbf{u}_1$ ve $\mathbf{u}_2$. Bu ayrışımda kırmızı ile gösterilen eksenleri ters yöne çevirseydik, yani $\mathbf{U}=\begin{bmatrix} \mathbf{u}_1 &  -\mathbf{u}_2\end{bmatrix}$ ve $\mathbf{V}=  \begin{bmatrix} \mathbf{v}_1 &  -\mathbf{v}_2\end{bmatrix}$ olsaydı $\mathbf{A} = \mathbf{U}\mathbf{\Sigma} \mathbf{V}^{H}$ eşitliği korunurdu. Dolayısıyla tek bir ayrışım yok! Aynı indekse ait sağ ve sol tekil vektörleri birlikte ters yöne çevirince aynı çarpımı elde ederiz.

Bunun yanısıra birim matrise bakmak da aydınlatıcı olacak. Örneğin 2x2'lik gerçel birim matrisi şu biçimde ayrıştırabiliriz:

$$\begin{bmatrix}\ 1& 0 \\ 0& 1\end{bmatrix} = \begin{bmatrix}\ \cos(\theta)& -\sin(\theta) \\ \sin(\theta)& \cos(\theta)\end{bmatrix} \begin{bmatrix}\ 1& 0 \\ 0& 1\end{bmatrix}  \begin{bmatrix}\ \cos(\theta)&\sin(\theta) \\ -\sin(\theta)& \cos(\theta)\end{bmatrix}$$

Görüldüğü üzere ne yazık ki, birim çember için de tek bir çözüm yok, hatta sonsuz çözüm var. Yani tekil değer ayrışımı için ikinci maddeyi cebe atamayacağız. Fakat bu uygulamalarda bize bir sorun yaşatmayacak çünkü tekil vektörlerin yönleri değil doğrultuları önemli olacak. Birim matriste olduğu gibi tekil değerlerin aynı olması durumunda sonsuz çözüm olması da bizi üzmeyecek çünkü seçeceğimiz herhangi bir çözüm uygulamadaki ihtiyaçlara eşdeğer güçte cevap verecek.

Son sorunun cevabını matematiksel olarak incelemek bu yazının kapsamını aşacak. O sebeple TDA'yı bu denli güçlü kılan özelliği olarak kararlı bir ayrışım olduğunu bilmekle yetinelim. Deneylerdeki küçük nümerik farklar sonuçlarda beklenmedik zıplamalara sebep olmayacak ve analizleri güvenilir kılacak.

Dikey Baz Matrisler

Eldeki matrisi ifade etmek için şu ana kadar matrisi üç matrisin çarpımı biçiminde yazdık. Peki aynı matrisi alternatif bir yolla da elde edemez miydik? Hem de bu yol bize farklı yorumlama kapıları açacaksa hemen bakmakta fayda var. İşte size aynı formülün laciverti!

$$\mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^H = \sum\limits_{i=1}^n \sigma_i \mathbf{u}_i \mathbf{v}_i^H$$

Yukarıdaki formülde $n$. dereceden bir matrisi 1. dereceden ve birbirine dikey $n$ tane matrisin doğrusal birleşimi (lineer kombinasyonu) biçiminde yazdık. $\mathbf{A}$ matrisine en çok katkıda bulunan matris $\sigma_1\mathbf{u}_1 \mathbf{v}_1^H$ matrisi, çünkü en büyük tekil değer $\sigma_1$ ve $\mathbf{u}_i \mathbf{v}_i^H$ matrislerinin Frobenius normları 1.

Elimizdeki matrisi eşit büyüklükteki farklı legolardan oluşmuş bir oyuncak gibi düşünürsek, bir biçimde bu oyuncakta kullanılan parçaları bulduk ($\mathbf{u}_i \mathbf{v}_i^H$) ve onların hangi oranda kullanıldığını ($\sigma_i$) belirledik.

Sınırlı sayıda farklı lego parçası seçmek durumunda kalsaydınız oyuncağı olası en iyi şekilde yapabilmek için hangilerini seçerdiniz?

Sonraki yazıda kaldığımız yerden devam etmek üzere burada bırakalım. Beklerken legolar üstüne düşünedurun. Ya da maddenin yapıtaşları üstüne. Ya da birimsellik (modülarite) üstüne. Ve neden bu gizli parçaları öğrenmek istediğimiz üstüne...