Çizimlerle Merkezi Limit Teoremi - 2

Geçtiğimiz yıl, merkezi limit teoremini çizimler eşliğinde gözlemlemiştik. Gelin bugün de bunu MATLAB'da yapalım.

Öncelikle $n$ tane bağımsız ve özdeşçe dağılmış değişken çekelim. Bunlar $x_i, i=\{1,\ldots,n\}$ ile gösterilsin. Ardından bunların ortalamasını alalım; bu da $y$ olsun.

\begin{align}
y = \frac{1}{n}\sum_{i=1}^n x_i
\end{align}

Hedefimiz $y$'lerin dağılımı gözlemlemek. Not etmekte fayda var. İlk yazıda değişkenlerin toplamlarına bakmıştık. Ortalaması ile toplamlarının aynı dağılımdan geldiği açık, yalnızca ölçekleri farklı. Dolayısıyla ortalamayı kullanmamızda bir sakınca yok. Hatta güven aralığını görmek açısından daha da iyi olacak, bekleyin...

Bir tane $y$ üretmek yetmez, bunlardan $m$ adet üretelim ve histogramına bakalım. MATLABca konuşursak, önce $m$ ve $n$'yi belirleyelim:

m = 10000; % Deney sayısı
n = 100; % Her deneyde ortalaması alınan rastsal değişken sayısı

Ardından $m$ adet $y$ hesaplayalım:

y = zeros(1,m);
for i = 1:m
    x = random('Uniform',0,1,[1 n]); % Birörnek dağılım
    % x = random('Binomial',203,0.98,[1 n]); % Binom dağılımı
    % x = random('Exponential',5,[1 n]); % Üssel dağılım
    % x = random('Poisson',3,[1 n]); % Poisson dağılımı
    % x = random('Normal',5,3,[1 n]); % Normal dağılım
    y(i) = sum(x)/n;
end

Burada birkaç tane olasılık dağılımı örneği koydum. İstediğinizi deneyebilirsiniz. Üstte $[0,1]$ arasında birörnek değerler üreten dağılımı kullandık.

Şimdi bu $y$'lerin histogramını çizelim:

[f,z] = hist(y,50);
bar(z,f/trapz(z,f)); % Düzgelenmiş histogramı çizelim

Hangi sorunun peşindeydik? Merkezi limit teoreminin dediğini hatırlayalım: $n$ değerini büyütürsek, $x_i$'lerin dağılımı ne olursa olsun, $y$'ler normal dağılıma yakınsayacak. Gerçekten de bu ortalamalar normal dağılımdan mı geliyor? Öyle olsaydı nasıl bir olasılık dağılım fonksiyonu olurdu? Bunu hesaplayıp histogramın üstüne çizelim:

mu = mean(y);
s = var(y);
g = 1/sqrt(2*pi*s)*exp(-0.5*(x-mu).^2/s);
hold on
plot(x,g,'r','Linewidth',3);
hold off

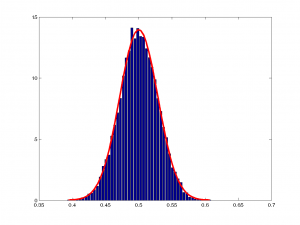
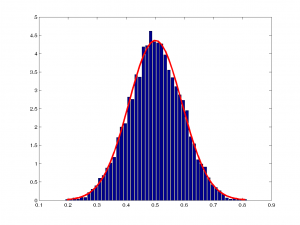
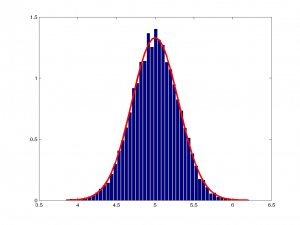
Bakalım $m=10000$, $n=100$ için bu çizim nasıl oldu:

İşte, gerçekten de beklediğimiz normal dağılımla örtüşen bir histogram çıktı!

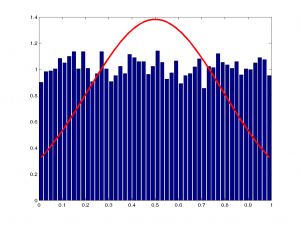
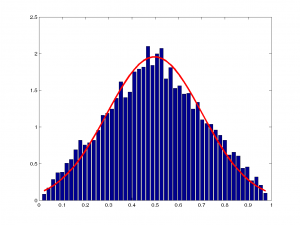
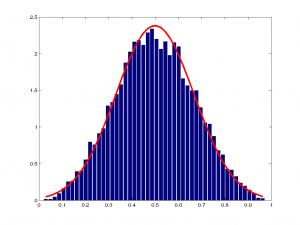
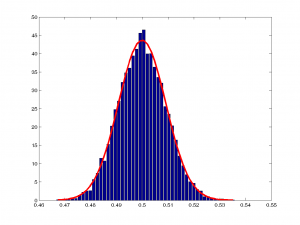
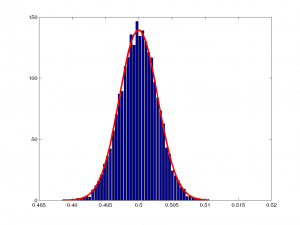
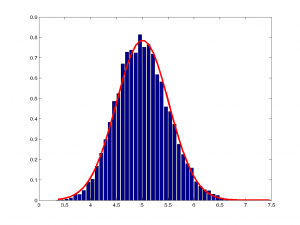
Şimdi altta, sırasıyla $n=1,2,3,10,100,1000$ ve $10000$ değerleri için hazırladığım çizimlere bakalım. Hatırlayalım, $n$ kaç tane değerin ortalamasını aldığımızı gösteriyordu:

Resimlerin üstüne tıklayarak ayrıntılı bakabilirsiniz. Burada dikkatinizi çeken bir şey olmalı. Tüm çizimlerde ortalama $y$ 0.5 iken, varyans farklı farklı. $n$ değeri büyüdükçe varyans küçülüyor. Demek ki daha çok örneğe baktığımızda beklenen ortalama değerin varyansı düşecek, yani daha güvenilir bir ortalama gözlemleyeceğiz.

Örneğin 20-25 yaş arası erkeklerin ayak numaralarının ortalamasını bilmek istiyorsunuz. Bu yaş aralığında 10 kişinin ayak numarasını sorup $y_{10}$ değerini buldunuz. Arkadaşınız da 1000 kişiye sordu ve $y_{1000}$ değerini buldu. Sizin bulduğunuz değer mi daha güvenilir, arkadaşınızınki mi? Elbette arkadaşınızınki, çünkü onun bulduğu ortalamanın varyansı daha düşük.

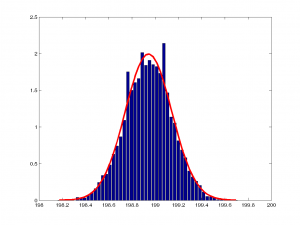
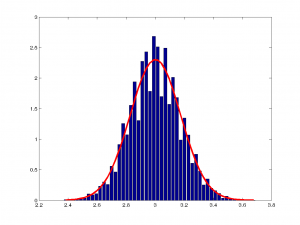
Şimdi bakmadığımız diğer çizimlere bakalım. $m=10000$ ve $n=100$ için sırasıyla binom, üssel, poisson ve normal dağılımlar için sonuçları çizelim: